Trong kho tàng kiến thức hình học hiện nay có vô vàn các khái niệm mà bạn cần nắm rõ. Trong đó trực tâm chính là một trong những khái niệm mà bạn sẽ bắt gặp khá thường xuyên. Vậy trực tâm là gì? Trực tâm có tính chất như thế nào? Tính trực tâm ra sao đảm bảo chuẩn xác nhất? Hãy cùng Blog Hỏi Ngu tìm hiểu!.
Nội dung chính:
Trực tâm là gì?
Trong một hình tam giác sẽ có rất nhiều các yếu tố mà bạn cần quan tâm. Đặc biệt khi bạn đang tìm hiểu về tam giác thì chắc chắn sẽ phải biết được trực tâm là gì. Trực tâm theo đó chính là giao điểm của 3 đường cao trong tam giác. Mỗi tam giác bất kỳ đều có 3 đường cao nhất định. Vì vậy để xác định trực tâm thì bạn cần phải xác định đường cao của tam giác.
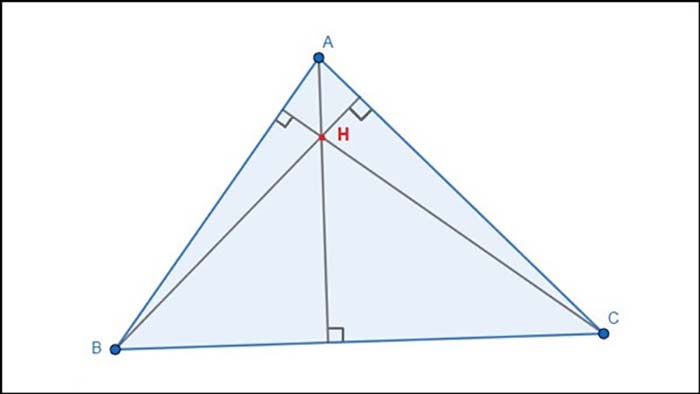
Trực tâm chính là điểm giao nhau của 3 đường cao trong tam giác
Đường cao trong tam giác chính là một đoạn thẳng được kẻ từ một đỉnh và đường thẳng này sẽ phải vuông góc với cạnh đối diện. Phần cạnh đáy đối diện này chính là đáy tương ứng với mỗi đường cao cụ thể. Việc xác định được đường cao sẽ giúp bạn có được trực tâm chuẩn xác nhất.
Trực tâm trong tam giác có những tính chất cơ bản nào?
Trực tâm của tam giác sẽ có những tính chất nhất định. Những tính chất này giúp bạn có thể hiểu hơn về trực tâm cũng như giúp bạn tính toán chuẩn xác nhất những phép tính liên quan. Vì vậy, theo kiến thức hình học cơ bản, trực tâm của tam giác có những tính chất sau:
-
Tính chất 1: Đối với một tam giác cân thì đường trung trực được xác định tương ứng với cạnh đáy. Ngoài ra đường trung trực trong tam giác cân cũng chính là đường cao, đường phân giác, đường trung tuyến của tam giác đó.
-
Tính chất 2: Nếu như đường trung tuyến đồng thời cũng chính là đường phân giác thì sẽ biết được tam giác bất kỳ đó chính là tam giác cân.
-
Tính chất 3: Nếu đường trung tuyến đồng thời là đường trung trực thì sẽ giúp bạn biết được tam giác bất kỳ đó cũng chính là tam giác cân.
-
Tính chất 4: Trong một tam giác nhọn, trực tâm sẽ chính là tâm của đường tròn nội tiếp tam giác với ba đỉnh được xác định chính là chân của ba đường cao. Các đường cao này sẽ được nối từ đỉnh A, B, C đến các cạnh đối diện tương ứng như BC, AC, AB.
-
Tính chất 5: Đường cao trong tam giác khi ứng với một đỉnh được xác định bằng cách cắt đường tròn ngoại tiếp tại một điểm thứ 2 sẽ được gọi là đối xứng của trực tâm thông qua cạnh tương ứng.
Thông qua những tính chất trên có thể thấy rằng, trực tâm, trọng tâm hay các điểm trong một tam giác đều đều cách đều 3 đỉnh, 3 cạnh. Các điểm này sẽ đều trùng với nhau tại một điểm cụ thể.
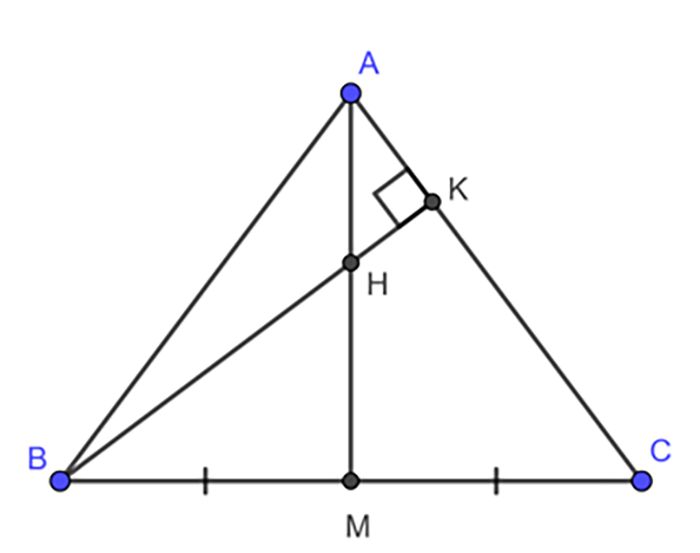
Vẽ hai đường cao giúp bạn xác định được ngay trực tâm ở vị trí nào
Cách tính trực tâm là gì chuẩn xác nhất?
Việc xác định trực tâm là cực kỳ quan trọng. Chính vì vậy ngoài việc biết được trực tâm là gì thì bạn cũng cần nắm được cách tính và cách xác định trực tâm trong tam giác. Theo đó, trực tâm chính là điểm giao nhau của ba đường cao trong cùng một tam giác. Vì vậy mà để xác định trực tâm thay vì phải vẽ 3 đường cao thì bạn chỉ cần vẽ 2 đường cao.
Đối với tam giác tù, tam giác nhọn hay tam giác cân thì xác định trực tâm đều như nhau là vẽ đường cao. Theo đó, từ hai đỉnh của tam giác bạn tiến hành vẽ một đường thẳng tới cạnh đối diện và vuông góc. Điểm giao nhau của hai đường cao chính là trực tâm của tam giác.
Có thể thấy, việc xác định trực tâm của tam giác không hề khó. Vì vậy khi biết được trực tâm là gì cũng như tính chất của chúng sẽ giúp bạn thao tác xác định trực tâm được dễ dàng hơn.



